塾生の質問から
伊勢高文系3年生のMちゃんから質問された問題がこちら。
$ 31^{17} $を $900$で割った余りを求めよ
定番問題と言えるのですが、文系の生徒には難しいかもしれません。
数学で一口に難問といっても何がどう難しいかは色々なタイプがあります。今回の場合は「とっかかり」が分かりづらいです。二次関数、三角関数、確率、微分・積分、ベクトル、数列など、どの範囲の問題かがハッキリすると解法の糸口がつかめたり思考を巡らしたりできます。それが見えにくいのです。この問題を見て『二項定理を利用する』と気づけるには類題を解いた経験が必要でしょうね。しいて言えば数字の特徴として$900=30^2$、$30+1=31$の関係(←これ自体気づきにくい)がヒントといえます。それから、二項定理を利用するときに頻出の関係式があります。
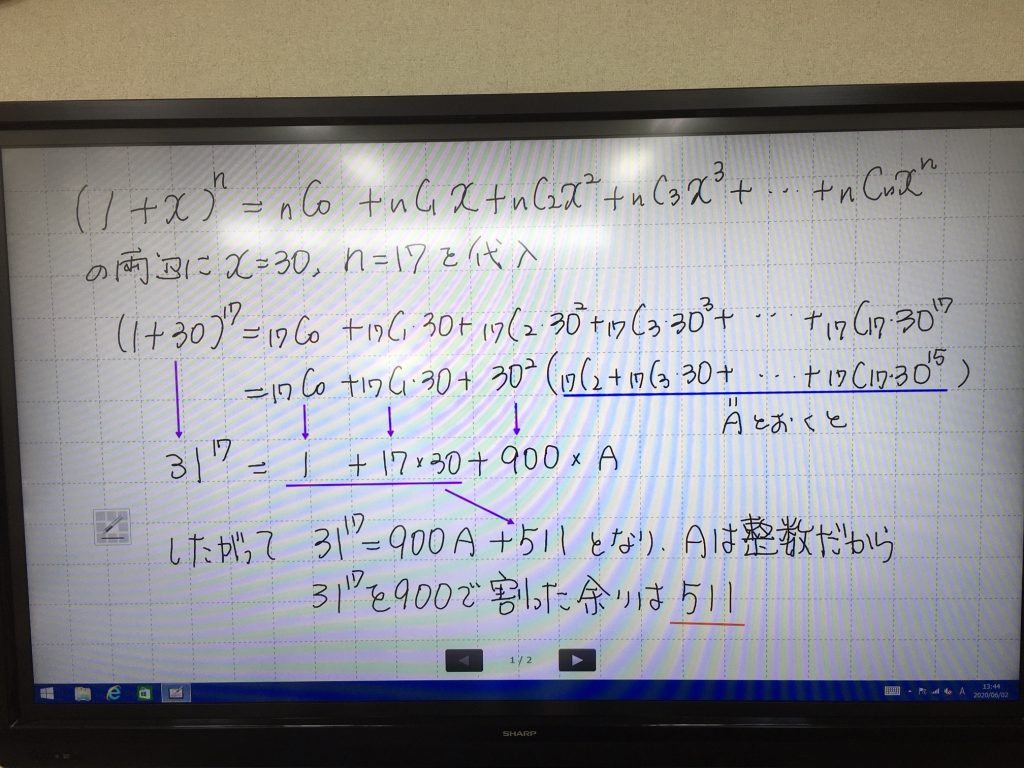
$$(1+x)^n=\begin{eqnarray*} && {}_n \mathrm{C} _0 + && {}_n \mathrm{C} _1・x + && {}_n \mathrm{C} _2・x^2 + && {}_n \mathrm{C} _3・x^3 + ・・・・ + && {}_n \mathrm{C} _n・x^n \end{eqnarray*}$$この等式は利用価値が高いので必ず覚えておくことと関連問題をたくさん演習するとよいですよ。
それでは問題の解法です。上の等式の両辺に$x=30,n=17$を代入すると左辺は問題の数式である$31^{17}$になります。あとは右辺を一工夫(変形)することで$900$の余りを求めることができます。変形の考え方ですが、右辺の第3項に$30^2(=900)$があり、第4項~末項にも$30^2$を因数に持つことがわかります。つまり第3項以降はすべて$900$で割り切れますから、余りは第1と第2の2つの項の和だけを対象にして求められます。