新しい角度の表し方
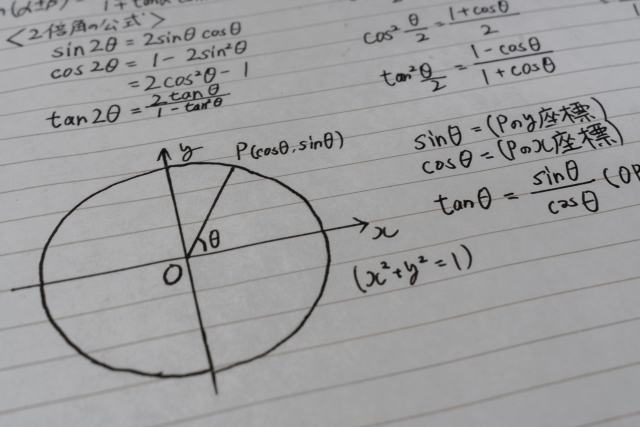
伊勢市*数学*塾・予備校*エムジェック*塾長の真鍋です。上空に最大級の寒波がいます。受験生のみなさん、体調をくずさないよう十分気をつけてください。
伊勢高一年生が三角関数(数Ⅱ)に入りました。角度の表し方として弧度法が登場します。日常生活で使うことのない弧度法をなぜ学習するのでしょうか。
結論は
弧度法は「三角関数を式で扱うときに自然でシンプルになる」表し方だから
弧度法は「円の大きさ」と直結
度数法は1周=360°(人が決めた約束)
一方、弧度法は 角=円周上の長さ ÷ 半径という定義です。
つまり、弧度法の角度は「円の一部がどれだけの長さか」をそのまま表す図形的にとても自然な量なのです。
公式が「きれい」になる
たとえば、円の半径を 、中心角を
として
弧度法:弧の長さ=
度数法:弧の長さ=
👉 弧度法では 余計な定数が消える
高校以降の数学では「三角関数の公式」「微分・積分」「物理の波や回転」などで式の単純さが非常に重要
三角関数の変化を正しく表せる
例えば有名な極限
これは弧度法のときだけ成り立つ関係です。
物理・工学では弧度法が「標準」
・角速度 ・振動、波動 ・回転運動 これらはすべて 弧度法が前提。
理由は単純で「長さ・時間・速さ」と同じ感覚で角を扱えるからです。
まとめ
度数法は「角度を数える方法」
弧度法は「円の大きさをそのまま表す方法」
数学では後者のほうが、公式が自然で、計算も楽になります。

